沐鸣注册
EM算法最初用于缺失数据模型参数估计, 现在已经用在许多优化问题中。 设模型中包含\(\boldsymbol X_{ ext{obs}}\)和\(\boldsymbol X_{ ext{mis}}\)两个随机成分, 有联合密度函数或概率函数\(f(\boldsymbol x_{ ext{obs}}, \boldsymbol x_{ ext{mis}} | \boldsymbol heta)\), \(\boldsymbol heta\)为未知参数。 称\(f(\boldsymbol x_{ ext{obs}}, \boldsymbol x_{ ext{mis}} | \boldsymbol heta)\)为完全数据的密度, 一般具有简单的形式。 实际上我们只有\(\boldsymbol X_{ ext{obs}}\)的观测数据\(\boldsymbol X_{ ext{obs}}=\boldsymbol x_{ ext{obs}}\), \(\boldsymbol X_{ ext{mis}}\)不能观测得到, 这一部分可能是缺失观测数据, 也可能是潜在影响因素。 所以实际的似然函数为 \[\begin{align} L(\boldsymbol heta)=f(\boldsymbol x_{ ext{obs}}|\boldsymbol heta)=\int f(\boldsymbol x_{ ext{obs}}, \boldsymbol x_{ ext{mis}} | \boldsymbol heta) \,d \boldsymbol x_{ ext{mis}}, ag{39.4} \end{align}\] 这个似然函数通常比完全数据的似然函数复杂得多, 所以很难直接从\(L(\boldsymbol heta)\)求最大似然估计。
EM算法的想法是, 已经有了参数的近似估计值\(\boldsymbol heta^{(t)}\)后, 假设\((\boldsymbol X_{ ext{obs}},\boldsymbol X_{ ext{mis}})\) 近似服从完全密度\(f(\boldsymbol x_{ ext{obs}}, \boldsymbol x_{ ext{mis}} | \boldsymbol heta^{(t)})\), 这里\(\boldsymbol X_{ ext{obs}}=\boldsymbol x_{ ext{obs}}\)已知, 所以认为\(\boldsymbol X_{ ext{mis}}\)近似服从由\(f(\boldsymbol x_{ ext{obs}}, \boldsymbol x_{ ext{mis}} | \boldsymbol heta^{(t)})\) 导出的条件分布 \[\begin{aligned} f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta^{(t)})=& \frac{f(\boldsymbol x_{ ext{obs}}, \boldsymbol x_{ ext{mis}} | \boldsymbol heta^{(t)})} {f(\boldsymbol x_{ ext{obs}}| \boldsymbol heta^{(t)})}, \end{aligned}\] 其中\(f(\boldsymbol x_{ ext{obs}}| \boldsymbol heta^{(t)})\)是由\(f(\boldsymbol x_{ ext{obs}}, \boldsymbol x_{ ext{mis}} | \boldsymbol heta^{(t)})\)决定的边缘密度。 据此近似条件分布, 在完全数据对数似然函数\(\log f(\boldsymbol X_{ ext{obs}}, \boldsymbol X_{ ext{mis}} | \boldsymbol heta)\)中, 把\(\boldsymbol X_{ ext{obs}}=\boldsymbol x_{ ext{obs}}\)看成已知, 关于未知部分\(\boldsymbol X_{ ext{mis}}\)按密度\(f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta^{(t)})\)求期望, 得到\(\boldsymbol heta\)的函数\(Q_t(\boldsymbol heta)\), 再求\(Q_t(\boldsymbol heta)\)的最大值点作为下一个\(\boldsymbol heta^{(t+1)}\)。
EM算法每次迭代有如下的E步(期望步)和M步(最大化步):
- E步: 计算完全数据对数似然函数的期望 \(Q_t(\boldsymbol heta)=E \big\{ \log f(\boldsymbol x_{ ext{obs}}, \boldsymbol X_{ ext{mis}} | \boldsymbol heta) \}\), 其中期望针对随机变量\(\boldsymbol X_{ ext{mis}}\), 求期望时假定\(\boldsymbol X_{ ext{mis}}\) 服从条件密度\(f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta^{(t)})\)决定的分布。
- M步: 求\(Q_t(\boldsymbol heta)\)的最大值点,记为\(\boldsymbol heta^{(t+1)}\), 迭代进入下一步。
定理39.1 EM算法得到的估计序列\(\boldsymbol heta^{(t)}\) 使得(39.4)中的似然函数值\(L(\boldsymbol heta^{(t)})\)单调不减。
证明: 对任意参数\(\boldsymbol heta\),有 \[\begin{aligned} \ln L( heta)=& \ln f(\boldsymbol x_{ ext{obs}} | heta) \cdot \int f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta^{(t)}) \,d \boldsymbol x_{ ext{mis}} \\=& \int \big[ \log f(\boldsymbol x_{ ext{obs}}, \boldsymbol x_{ ext{mis}} | \boldsymbol heta) - \log f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta) \big] f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta^{(t)}) \,d\boldsymbol x_{ ext{mis}} \\=& \int \log f(\boldsymbol x_{ ext{obs}}, \boldsymbol x_{ ext{mis}} | \boldsymbol heta) f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta^{(t)}) \,d\boldsymbol x_{ ext{mis}} \\ & - \int \log f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta) f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta^{(t)}) \,d\boldsymbol x_{ ext{mis}} \\=& Q_t(\boldsymbol heta) - \int \log f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta) f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta^{(t)}) \,d\boldsymbol x_{ ext{mis}} \end{aligned}\] 由信息不等式知 \[\begin{aligned} &\int \log f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta) f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta^{(t)}) \,d\boldsymbol x_{ ext{mis}} \\ \leq& \int \log f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta^{(t)}) f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta^{(t)}) \,d\boldsymbol x_{ ext{mis}} \end{aligned}\] 又EM迭代使得\(Q_t(\boldsymbol heta^{(t+1)}) \geq Q_t(\boldsymbol heta^{(t)})\), 所以 \[\begin{aligned} \log L(\boldsymbol heta^{(t+1)}) \geq & Q_t(\boldsymbol heta^{(t)}) - \int \log f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta^{(t)}) f(\boldsymbol x_{ ext{mis}} | \boldsymbol x_{ ext{obs}}, \boldsymbol heta^{(t)}) \,d\boldsymbol x_{ ext{mis}} \\=& \log L(\boldsymbol heta^{(t)}) . \end{aligned}\] 定理证毕。
※※※※※
在适当正则性条件下, EM算法的迭代序列\(\boldsymbol heta^{(t)}\)依概率收敛到\(L(\boldsymbol heta)\) 的最大值点\(\hat{\boldsymbol heta}\)。 但是, 定理39.1仅保证EM算法最终能收敛, 但不能保证EM算法会收敛到似然函数的全局最大值点, 算法也可能收敛到局部极大值点或者鞍点。
在实际问题中, 往往E步和M步都比较简单, 有时E步和M步都有解析表达式, 这时EM算法实现很简单。 EM算法优点是计算稳定, 可以保持原有的参数约束, 缺点是收敛可能很慢, 尤其是接近最大值点时可能收敛更慢。 如果(39.4)中的似然函数不是凸函数, 算法可能收敛不到全局最大值点, 遇到这样的问题可以多取不同初值比较, 用矩估计等合适的近似值作为初值。
例39.3 (多项分布) 设\(X\)取值于\(\{1,2,3,4 \}\), 分布概率为\(p(x | heta) \stackrel{ riangle}{=} \pi_x( heta)\): \[\begin{aligned} \pi_1( heta)=& \frac14 (2 + heta), & \pi_2( heta)=& \frac14 (1 - heta), \\ \pi_3( heta)=& \frac14 (1 - heta), & \pi_4( heta)=& \frac14 heta . \end{aligned}\] 设\(n\)次试验得到的\(X\)值有\(n_j\)个\(j\)(\(j=1,2,3,4\)), 求参数\( heta\)的最大似然估计。
这是 (Dempster, Lairdk, and Rubin 1977) 文章中的例子。 观测数据的对数似然函数为(去掉了与参数无关的加性常数) \[\begin{align*} l( heta)=n_1 \log(2+ heta) + (n_2 + n_3) \log(1- heta) + n_4 \log heta . \end{align*}\]
令\(l'( heta)=0\)得到一个关于\( heta\)的二次方程, 由此写出\(\mathop{ ext{argmax}} l( heta)\)的解析表达式:
\[ l'( heta)=\frac{n_1}{2+ heta} - \frac{n_2 + n_3}{1- heta} + \frac{n_4}{ heta} \] 令\(l'( heta)=0\),即求解二次方程 \[ n heta^2 + (-n_1 + 2n_2 + 2n_3 + n_4) heta - 2 n_4=0 . \] 得最大似然估计为 \[ \hat heta=\frac{-b + \sqrt{b^2 + 8 n n_4}}{2n} \] 其中\(b=-n_1 + 2n_2 + 2n_3 + n_4\)。
例如, \(n=400\), \(n_1=80\), \(n_2=120\), \(n_3=110\), \(n_4=90\)时:
下面用EM算法迭代估计\( heta\)。 将结果1分解为11和12, \(n_1\)分解为\(Z_1 + Z_2\), 其中\(P(X=11)=\frac12\), \(P(X=12)=\frac14 heta\)。 这时\(Z_2 + n_4\)代表结果12和结果4的出现次数, 这两种结果出现概率为\(\frac12 heta\), 其它结果(11, 2, 3)的出现概率为\(1 - \frac12 heta\)。 令\(Y=Z_2 + n_4\),则\(Y \sim ext{B}(n, \frac12 heta)\)。
数据\((Z_1, Z_2, n_2, n_3, n_4)\)的全似然函数为 \[ L_c( heta) \propto (\frac12)^{Z_1} (\frac{ heta}{4})^{Z_2} (\frac14 - \frac{ heta}{4})^{n_2 + n_3} (\frac{ heta}{4})^{n_4} \] 对数似然函数(差一个与\( heta\)无关的常数项)为 \[ l_c( heta)=\ln L_c( heta)=(Z_2 + n_4) \ln heta + (n_2 + n_3) \ln(1 - heta) \]
在EM迭代中, 假设已经得到的参数\( heta\)近似值为\( heta^{(t)}\), 设\( heta= heta^{(t)}\), 在给定\(n, n_1, n_2, n_3, n_4\)条件下求\(l_c( heta)\)的条件期望, 这时\(Z_2\)的条件分布为 \[ ext{B} \left( n_1, \frac{ heta^{(t)}}{2 + heta^{(t)}} \right) , \] 于是 \[ Z_2^{(t)}=E(Z_2 | heta^{(t)}, n, n_1, n_2, n_3, n_4)=n_1 \frac{ heta^{(t)}}{2 + heta^{(t)}} , \] 从而完全对数似然函数的条件期望为 \[ Q_t( heta)=E(\ln L_c( heta) | heta^{(t)}, n, n_1, n_2, n_3, n_4)=(Z_2^{(t)} + n_4) \ln heta + (n_2 + n_3) \ln(1 - heta) . \] 求解\(Q_t( heta)\)的最大值, 令 \[ \frac{d}{d heta} Q_t( heta)=\frac{n_4 + Z_2^{(t)}}{ heta} - \frac{n_2 + n_3}{1 - heta}=0 , \] 得下一个参数近似值为 \[ heta^{(t+1)}=\frac{n_4 + Z_2^{(t)}}{n_2 + n_3 + n_4 + Z_2^{(t)}} . \]
于是, EM迭代步骤从某个\( heta^{(0)}\)出发, 比如\( heta^{(0)}=\frac12\), 在第\(t\)步计算 \[ Z_2^{(t)}=n_1 \frac{ heta^{(t)}}{2 + heta^{(t)}}, \quad heta^{(t+1)}=\frac{n_4 + Z_2^{(t)}}{n_2 + n_3 + n_4 + Z_2^{(t)}} \] 迭代到两次的近似参数值变化小于\(\epsilon=10^{-6}\)为止。
程序例:
仅需要6次迭代就达到了小数点后6位精度。
※※※※※
例39.4 (指数分布右删失(*)) 设某种设备的寿命总体\(Y \sim ext{Exp}(1/ heta)\), \(EY= heta\), 对\(n\)个这样的设备进行寿命试验, 其中\(n_1\)个观测到失效时间\(t_1, \dots, t_{n_1}\), 另外的\(n_2=n - n_1\)个没有观测到失效, 仅知道失效时间分别超过\(c_j, j=n_1+1, \dots, n\)。 求参数的最大似然估计。
观测数据为 \[ \boldsymbol x=(x_1, \dots, x_{n_1}, x_{n_1 + 1}, \dots, x_n)=(t_1, \dots, t_{n_1}, c_{n_1+1}, \dots, c_n) \] 观测数据的似然函数为 \[ L( heta)=(\frac{1}{ heta})^{n_1} \exp\{ -\frac{1}{ heta} \sum_{1}^{n_1} t_i \} \exp\{ -\frac{1}{ heta} \sum_{n_1+1}^n c_j \}= heta^{-n_1} \exp\{ -\frac{1}{ heta} \sum_{1}^n x_i \} \] 对数似然函数为 \[ \ln L( heta)=-n_1 \ln heta - \frac{1}{ heta} \sum_1^n x_i \] 令\(\frac{d}{d heta} \ln L( heta)=0\)得最大似然估计为 \[ \hat heta=\frac{1}{n_1} \sum_{i=1}^n x_i \]
下面用EM算法估计\( heta\)。 设完全数据为\((t_1, \dots, t_{n_1}, t_{n_1+1}, \dots, t_n)\)都是失效时间, 完全数据的似然函数为 \[ L_c( heta)= heta^{-n} \exp\{ -\frac{1}{ heta} \sum_1^n t_i \} \] 完全的对数似然函数为 \[ \ln L_c( heta)=-n \ln heta - \frac{1}{ heta} \sum_1^{n_1} t_i - \frac{1}{ heta} \sum_{n_1+1}^{n} t_j \]
取适当初值\( heta^{(0)}\), 如\( heta^{(0)}=\frac{1}{n} x_i\)。 在迭代中设已有\( heta^{(t)}\), 在已知\( heta= heta^{(t)}\), \(t_i, i=1,\dots, n_1\), \(t_j > c_j, j=n_1+1, \dots, n\)的条件下求\(\ln L_c( heta)\)的条件期望, 先求 \(E(t_j | heta^{(t)}, t_j > c_j)\),\(j=n_1+1, \dots, n\)。 易见\(t_j - c_j\)的条件分布为\( ext{Exp}(\frac{1}{ heta^{(t)}})\),所以 \[ E(t_j | heta^{(t)}, t_j > c_j)=c_j + E(t_j - c_j | heta^{(t)}, t_j > c_j)=c_j + heta^{(t)} \] 所以 \[ \begin{aligned} Q_t( heta)=& E \left[ \ln L_c( heta) \;|\; \boldsymbol x \right]=-n \ln heta - \frac{1}{ heta} \sum_{1}^{n_1} t_i - \frac{1}{ heta} \sum_{n_1}^n (c_j + heta^{(t)}) \\=& -n \ln heta - \frac{1}{ heta} \sum_{1}^{n} x_i - n_2 \frac{ heta^{(t)}}{ heta} \end{aligned} \] 令\(\frac{d}{d heta} Q_t( heta)=0\)得参数的迭代公式为 \[ heta^{(t+1)}=\frac{1}{n} \left( \sum_{1}^n x_i + n_2 heta^{(t)} \right) \]
模拟实例:
※※※※※
例39.5 (另一指数分布右删失) 设某种设备的寿命总体\(Y \sim ext{Exp}(1/ heta)\), \(EY= heta\), 设对\(n\)个这样的设备进行寿命试验, 得到了失效时间\(x_1, \dots, x_n\), 对另外的\(m\)个这样的设备进行寿命试验, 仅知道其中\(r\)个在时刻\(s\)之前失效, \(m-r\)个未失效。 用EM方法求\( heta\)的最大似然估计。
观测数据为 \[ \boldsymbol x=(x_1, \dots, x_{n}, r), \] 观测数据的似然函数为 \[ L( heta) \propto heta^{-n} \exp\{ -\frac{1}{ heta} \sum_1^n x_i \} (1 - e^{-s/ heta})^r e^{-(m-r)s/ heta} , \] 对数似然函数为 \[ \ln L( heta)=-n\ln heta + r \ln(1 - e^{-s/ heta}) - \frac{1}{ heta} \left[\sum_1^n x_i + (m-r)s \right] , \] 直接求MLE有困难。
下面用EM算法估计\( heta\)。 设第二批的\(m\)个试验的具体失效时间为\(u_j, j=1,\dots, m\)。 完全数据的似然函数为 \[ L_c( heta)= heta^{-n-m} \exp\left\{ -\frac{1}{ heta} \left[ \sum_1^n x_i + \sum_1^m u_j \right] \right\} , \] 完全的对数似然函数为 \[ \ln L_c( heta)=-(n+m) \ln heta -\frac{1}{ heta} \left[ \sum_1^n x_i + \sum_1^m u_j \right] . \]
取适当初值\( heta^{(0)}\), 如\( heta^{(0)}=\frac{1}{n} x_i\)。 在迭代中设已有\( heta^{(t)}\), 在已知\( heta= heta^{(t)}\)和观测数据\(\boldsymbol x\)的条件下求\(\ln L_c( heta)\)的条件期望。 先求 \(E(u_j | heta^{(t)}, \boldsymbol x)\),\(j=n_1+1, \dots, n\)。 在给定\( heta= heta^{(t)}\), 观测数据\(\boldsymbol x\)和\(u_j < s\)条件下, \(u_j\)的条件分布是Exp\((1/ heta^{(t)})\)在\(u_j < s\)下的条件分布, \[ P(u_j > u | u_j < s)=\frac{P(u < u_j < s)}{P(u_j < s)}=\frac{e^{-u/ heta^{(t)}} - e^{-s/ heta^{(t)}}}{1 - e^{-s/ heta^{(t)}}} , \] 这时 \[ E(u_j | heta^{(t)}, u_j < s)=\int_0^s P(u_j > u | u_j < s) \,du= heta^{(t)} + s - \frac{s}{1 - e^{-s/ heta^{(t)}}} . \] 在给定\( heta= heta^{(t)}\),观测数据\(\boldsymbol x\)和\(u_j \geq s\)条件下, \(u_j - s\)条件分布是Exp\((1/ heta^{(t)})\), 所以 \[ E(u_j | heta^{(t)}, u_j \geq s)=s + heta^{(t)} . \] 于是 \[ \begin{aligned} E(u_j | heta^{(t)}, \boldsymbol x)=& E(u_j | heta^{(t)}, u_j < s) P(u_j < s) + E(u_j | heta^{(t)}, u_j \geq s) P(u_j \geq s) \\=& \left( heta^{(t)} + s - \frac{s}{1 - e^{-s/ heta^{(t)}}} \right) \frac{r}{m} + (s + heta^{(t)}) \frac{m-r}{m} . \end{aligned} \] 所以 \[\begin{aligned} Q_t( heta)=& E \left[ \ln L_c( heta) | heta^{(t)}, \boldsymbol x \right] \\=& -(n+m) \ln heta - \frac{1}{ heta}\left[ \sum_1^n x_i \right. \\ & + \left. \left( heta^{(t)} + s - \frac{s}{1 - e^{-s/ heta^{(t)}}} \right) r + (s + heta^{(t)}) (m-r) \right] . \end{aligned}\] 求 \[\begin{aligned} & \frac{d}{d heta} Q_t( heta) \\=& - \frac{n+m}{ heta} + \frac{1}{ heta^2} \left[\sum_1^n x_i \right. \\ &+ \left. \left( heta^{(t)} + s - \frac{s}{1 - e^{-s/ heta^{(t)}}} \right) r + (s + heta^{(t)}) (m-r) \right] \\=& 0 , \end{aligned}\] 解得迭代公式为 \[ heta^{(t+1)}=\frac{1}{n+m} \left[ \sum_1^n x_i + m( heta^{(t)} + s) - \frac{rs}{1 - e^{-s/ heta^{(t)}}} \right] . \]
模拟实例:
图形验证:
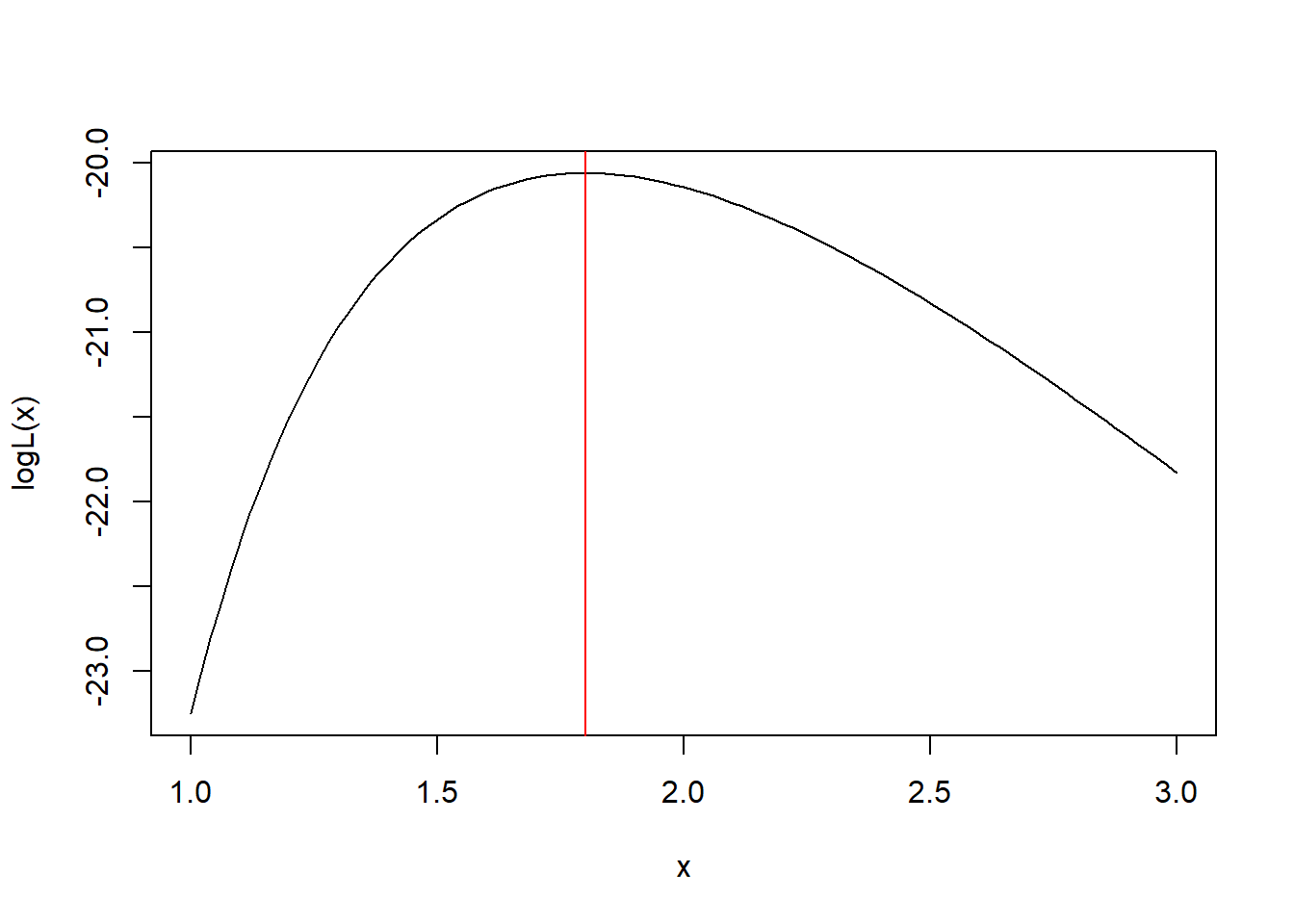
※※※※※
例39.6 (正态分布右删失(*)) 设总体为N(\( heta\),1)分布, 观测样本\(X_1, \dots, X_n\)有观测值\(x_1, \dots, x_n\), 另外有\(Z_1, \dots, Z_m\)仅知道\(Z_j > a\), \(j=1, \dots, m\), 称\(Z_j\)是右删失观测。假设这些观测都相互独立,则实际的似然函数为 \[\begin{align} L( heta)=f(\boldsymbol x | heta)=\left[ 1 - \Phi(a - heta) \right]^m \prod_{i=1}^n \phi(x_i - heta), \end{align}\] 其中\(\phi(\cdot)\)和\(\Phi(\cdot)\)分别为标准正态分布的分布密度和分布函数。
用EM算法求最大似然估计, 以\(\boldsymbol X=(X_1, \dots, X_n)\)为有观测的部分, 以\(\boldsymbol Z=(Z_1, \dots, Z_m)\)为没有观测的部分。 完全数据的联合密度为 \[\begin{aligned} f(\boldsymbol x, \boldsymbol z | heta)=\prod_{i=1}^n \phi(x_i - heta) \prod_{j=1}^m \phi(z_j - heta) . \end{aligned}\]
在E步, 设\( heta^{(t)}\)为参数的一个估计值, 在已知\(\boldsymbol X=\boldsymbol x\)条件下, \(\boldsymbol Z\)的条件密度可以从完全数据联合密度导出: \[\begin{aligned} f(\boldsymbol z | \boldsymbol x, heta^{(t)})=& \frac{f(\boldsymbol x, \boldsymbol z | heta^{(t)})}{f(\boldsymbol x | heta^{(t)})}=[ 1 - \Phi(a- heta^{(t)}) ]^{-m} \prod_{j=1}^m \phi(z_j - heta^{(t)}), \end{aligned}\] 这个条件分布可以看成是与\(\boldsymbol X\)独立, 且\(Z_1, \dots, Z_m\)独立, 有共同的条件密度\(\phi(z - heta^{(t)})/[1 - \Phi(a- heta^{(t)})]\), \(z > a\)。 求完全数据对数似然关于\(\boldsymbol Z\)的条件期望, 有 \[\begin{aligned} Q_t( heta)=& E \log \left[ \prod_{i=1}^n \phi(x_i - heta) \prod_{j=1}^m \phi(Z_j - heta) \right] \\=& \sum_{i=1}^n \log\phi(x_i - heta) + \sum_{j=1}^m E \log \phi(Z_j - heta), \end{aligned}\] 其中\(Z_j\)独立,有共同密度\(\phi(z - heta^{(t)})/[1 - \Phi(a- heta^{(t)})]\),\(z>a\), 所以 \[\begin{aligned} Q_t( heta)=& \sum_{i=1}^n \log\phi(x_i - heta) + m \int_a^\infty \log \phi(z - heta) \cdot \frac{\phi(z - heta^{(t)})}{1 - \Phi(a- heta^{(t)})} \,dz. \end{aligned}\]
在M步, 要求\(Q_t( heta)\)的最大值点。 注意\(\frac{d}{dx} \log \phi(x)=\phi'(x)/\phi(x)=-x\), 得 \[\begin{aligned} Q_t'( heta)=& \sum_{i=1}^n (x_i - heta) + m \int_a^\infty (z - heta) \frac{\phi(z - heta^{(t)})}{1 - \Phi(a- heta^{(t)})} \,dz \\=& n \bar X - n heta + m \int_a^\infty (z - heta^{(t)}) \frac{\phi(z - heta^{(t)})}{1 - \Phi(a- heta^{(t)})} \,dz + m ( heta^{(t)} - heta) \\=& n \bar X - n heta + m heta^{(t)} - m heta + m \frac{1}{1 - \Phi(a - heta^{(t)})}\int_{a - heta^{(t)}}^\infty u \phi(u) \,du \\ & \quad( ext{令}u=z - heta^{(t)}) \\=& -(n+m) heta + n \bar X + m heta^{(t)} + m \frac{\phi(a- heta^{(t)})}{1 - \Phi(a- heta^{(t)})} . \end{aligned}\] 令\(Q_t'( heta)=0\)得 \[\begin{align} heta^{(t+1)}=\frac{1}{n+m} \left[ n \bar X + m heta^{(t)} + m \frac{\phi(a- heta^{(t)})}{1 - \Phi(a- heta^{(t)})} \right] ag{39.5} \end{align}\] 为\(Q_t( heta)\)的最大值点。 选取适当初值\( heta^{(0)}\) 按(39.5)迭代就可以求得带有右删失数据的正态总体参数\( heta\)的最大似然估计。
※※※※※
例39.7 (混合分布) EM算法可以用来估计混合分布的参数。 设随机变量\(Y_1 \sim ext{N}(\mu_1, \delta_1)\), \(Y_2 \sim ext{N}(\mu_2, \delta_2)\), \(Y_1, Y_2\)独立。 记\(N(\mu,\delta)\)的密度为\(f(x|\mu, \delta)\)。 设随机变量\(W \sim ext{b}(1, \lambda)\), \(0<\lambda<1\), \(W\)与\(Y_1, Y_2\)独立,令 \[\begin{aligned} X=(1-W) Y_1 + W Y_2, \end{aligned}\] 则\(W=0\)条件下\(X \sim ext{N}(\mu_1, \delta_1)\), \(W=1\)条件下\(X \sim ext{N}(\mu_2, \delta_2)\), 但\(X\)的边缘密度为 \[\begin{aligned} f(x|\boldsymbol heta)=(1-\lambda) f(x|\mu_1, \delta_1) + \lambda f(x|\mu_2, \delta_2) , \end{aligned}\] 其中\(\boldsymbol heta=(\mu_1, \delta_1, \mu_2, \delta_2, \lambda)\)。
设\(X\)有样本\(\boldsymbol X=(X_1, \dots, X_n)\), 样本值为\(\boldsymbol x\), 实际观测数据的似然函数为 \[\begin{aligned} L(\boldsymbol heta)=\prod_{i=1}^n f(x_i|\boldsymbol heta) , \end{aligned}\] 这个函数是光滑函数但是形状很复杂, 直接求极值很容易停留在局部极值点。
用EM算法,以\(\boldsymbol W=(W_1, \dots, W_n)\)为没有观测到的部分, 完全数据的似然函数和对数似然函数为 \[\begin{aligned} ilde L(\boldsymbol heta | \boldsymbol x, \boldsymbol W)=& \prod_{W_i=0} f(x_i | \mu_1, \delta_1) \ \prod_{W_i=1} f(x_i | \mu_2, \delta_2) \ \lambda^{\sum_{i=1}^n W_i} (1-\lambda)^{n - \sum_{i=1}^n W_i} , onumber\\ ilde l(\boldsymbol heta | \boldsymbol x, \boldsymbol W)=& \sum_{i=1}^n \Big[ (1-W_i) \log f(x_i | \mu_1, \delta_1) + W_i \log f(x_i | \mu_2, \delta_2) \Big] onumber\\ & + \left(\sum_{i=1}^n W_i \right) \log \lambda + \left(n - \sum_{i=1}^n W_i \right) \log(1-\lambda) . \end{aligned}\]
在E步,设已有\(\boldsymbol heta\) 的近似值\(\boldsymbol heta^{(t)}=(\mu_1^{(t)}, \delta_1^{(t)}, \mu_2^{(t)}, \delta_2^{(t)}, \lambda^{(t)})\), 以\(\boldsymbol heta^{(t)}\)为分布参数,在\(\boldsymbol X=\boldsymbol x\)条件下, \(W_i\)的条件分布为 \[\begin{align} \gamma_i^{(t)} \stackrel{ riangle}{=} & P(W_i=1 | \boldsymbol x, \boldsymbol heta^{(t)})=P(W_i=1 | X_i=x_i, \boldsymbol heta^{(t)}) onumber\\=& \frac{\lambda^{(t)} f(x_i | \mu_2^{(t)}, \delta_2^{(t)})} { (1 - \lambda^{(t)}) f(x_i | \mu_1^{(t)}, \delta_1^{(t)}) + \lambda^{(t)} f(x_i | \mu_2^{(t)}, \delta_2^{(t)}) } . ag{39.6} \end{align}\] 这里的推导类似于逆概率公式。 利用\(W_i\)的条件分布求完全数据对数似然的期望,得 \[\begin{aligned} Q_t(\boldsymbol heta)=& \sum_{i=1}^n \left[ (1 - \gamma_i^{(t)}) \log f(x_i | \mu_1, \delta_1) + \gamma_i^{(t)} \log f(x_i | \mu_2, \delta_2) \right] onumber\\ & + \left(\sum_{i=1}^n \gamma_i^{(t)} \right) \log \lambda + \left(n - \sum_{i=1}^n \gamma_i^{(t)} \right) \log(1-\lambda) . \end{aligned}\]
令\( abla Q_t(\boldsymbol heta)=\boldsymbol 0\), 求得\(Q_t(\boldsymbol heta)\)的最大值点\(\boldsymbol heta^{(t+1)}\)为 \[\begin{align} \begin{cases} \mu_1^{(t+1)}=\frac{ \sum_{i=1}^n (1 - \gamma_i^{(t)}) x_i } { \sum_{i=1}^n (1 - \gamma_i^{(t)}) } \\ \delta_1^{(t+1)}=\frac{ \sum_{i=1}^n (1 - \gamma_i^{(t)}) (x_i - \mu_1^{(t+1)})^2 } { \sum_{i=1}^n (1 - \gamma_i^{(t)}) } \\ \mu_2^{(t+1)}=\frac{ \sum_{i=1}^n \gamma_i^{(t)} x_i } { \sum_{i=1}^n \gamma_i^{(t)} } \\ \delta_2^{(t+1)}=\frac{ \sum_{i=1}^n \gamma_i^{(t)}(x_i - \mu_2^{(t+1)})^2 } { \sum_{i=1}^n \gamma_i^{(t)} } \\ \lambda^{(t+1)}=\frac{1}{n} \sum_{i=1}^n \gamma_i^{(t)} \\ \end{cases} ag{39.7} \end{align}\] 适当选取初值\(\boldsymbol heta^{(0)}\)用(39.6)和(39.7)迭代就可以计算\(\boldsymbol heta\)的最大似然估计。
※※※※※





